- Přehledy IS
- APS (20)
- BPM - procesní řízení (23)
- Cloud computing (IaaS) (10)
- Cloud computing (SaaS) (33)
- CRM (51)
- DMS/ECM - správa dokumentů (20)
- EAM (17)
- Ekonomické systémy (68)
- ERP (77)
- HRM (28)
- ITSM (6)
- MES (32)
- Řízení výroby (36)
- WMS (29)
- Dodavatelé IT služeb a řešení
- Datová centra (25)
- Dodavatelé CAD/CAM/PLM/BIM... (39)
- Dodavatelé CRM (33)
- Dodavatelé DW-BI (50)
- Dodavatelé ERP (71)
- Informační bezpečnost (50)
- IT řešení pro logistiku (45)
- IT řešení pro stavebnictví (26)
- Řešení pro veřejný a státní sektor (27)
 ERP systémy
ERP systémy CRM systémy
CRM systémy Plánování a řízení výroby
Plánování a řízení výroby AI a Business Intelligence
AI a Business Intelligence DMS/ECM - Správa dokumentů
DMS/ECM - Správa dokumentů HRM/HCM - Řízení lidských zdrojů
HRM/HCM - Řízení lidských zdrojů EAM/CMMS - Správa majetku a údržby
EAM/CMMS - Správa majetku a údržby Účetní a ekonomické systémy
Účetní a ekonomické systémy ITSM (ITIL) - Řízení IT
ITSM (ITIL) - Řízení IT Cloud a virtualizace IT
Cloud a virtualizace IT IT Security
IT Security Logistika, řízení skladů, WMS
Logistika, řízení skladů, WMS IT právo
IT právo GIS - geografické informační systémy
GIS - geografické informační systémy Projektové řízení
Projektové řízení Trendy ICT
Trendy ICT E-commerce B2B/B2C
E-commerce B2B/B2C CAD/CAM/CAE/PLM/3D tisk
CAD/CAM/CAE/PLM/3D tisk| Přihlaste se k odběru newsletteru SystemNEWS, který každý týden přináší výběr článků z oblasti podnikové informatiky | |
 | |
Nejčastěji používané metody při analýze lékařských dat
 Statistické studie jsou v medicíně nutností. Velmi malá část lékařů zpracovává svoje data bez pomoci odborníka, statistika. Vyhledáním jeho pomoci ovšem práce odvedená lékařem nekončí. Oba totiž mluví každý naprosto odlišným jazykem, proto je pro správnost závěrů analýzy nezbytné, aby se domluvili a vzájemně pochopili. V tomto příspěvku se seznámíme s nejobvyklejšími statistickými postupy, které vyžaduje analýza dat z lékařského prostředí.
Statistické studie jsou v medicíně nutností. Velmi malá část lékařů zpracovává svoje data bez pomoci odborníka, statistika. Vyhledáním jeho pomoci ovšem práce odvedená lékařem nekončí. Oba totiž mluví každý naprosto odlišným jazykem, proto je pro správnost závěrů analýzy nezbytné, aby se domluvili a vzájemně pochopili. V tomto příspěvku se seznámíme s nejobvyklejšími statistickými postupy, které vyžaduje analýza dat z lékařského prostředí.


Před samotným sběrem dat je důležité zvážit, které parametry mohou mít souvislost se zkoumanými veličinami, a proto je vhodné je zaznamenávat. Kromě určení počtu parametrů je důležité také stanovit tzv. rozsah výběru, tedy kolik pacientů je třeba do studie zahrnout. Ze statistického pohledu je nutné, aby rozsah výběru byl tak velký, aby bylo dosaženo dostatečné síly testu, typicky kolem osmdesáti procent. Co to přesně znamená? Statistický test je ve své podstatě pravidlo, které na základě výsledků zjištěných ze vzorku dat předepisuje rozhodnutí o zamítnutí nebo nezamítnutí tzv. nulové hypotézy týkající se celé populace, z níž vzorek pochází. Závěry analýzy jsou platné vždy jen s určitou pravděpodobností, většinou je požadována pětiprocentní hladina testu povolující chybu, kdy dojde k zamítnutí ve skutečnosti platné nulové hypotézy maximálně v pěti procentech případů.
Síla testu je pak pravděpodobnost, že správně zamítneme nulovou hypotézu v případě, kdy opravdu neplatí. Pokud by byla síla testu malá, riskujeme, že neodhalíme neplatnost nulové hypotézy, a dojdeme tak k falešným závěrům. Vyšší rozsah výběru zpravidla vede k vyšší síle testu. Na druhou stranu je ale ekonomické, a proto žádoucí, aby rozsah výběru nebyl příliš velký. Pokud se analýza zabývá porovnáním nějakých skupin, je vhodné, aby tyto skupiny měly v ideálním případě stejný nebo podobný rozsah.
Přípravná fáze analýzy, bez ohledu na to, s jakým softwarem pracujeme, vyžaduje poměrně dobrou představu o metodách, které pro vyhodnocení získaných údajů použijeme, a také znalost principů a matematické podstaty těchto metod. Statistické programy umí určit potřebný rozsah vzorku pro velmi malou skupinu statistických testů (viz příklad možného výčtu testů na obrázku níže) a při jejich modifikaci je dobré do přípravné fáze zahrnout i konzultaci statistika. Obecně se stanovením velikosti vzorku zabývá část statistiky s názvem analýza síly testu (poweranalysis).
Jakmile jsou k dispozici záznamy, je třeba se v nich zorientovat a zkontrolovat, že neobsahují chyby nebo odlehlá pozorování. Pro tyto účely nabízejí statistické programy bezpočet různých grafů a testů nebo tabulek.
Jaké úlohy lékaři řeší?
Jednou z nejběžnějších otázek, na kterou lékaři potřebují odpověď, je porovnání dvou skupin pacientů například z hlediska výskytu komplikací po operacích. Například zda konkrétní typ operace provedené týmem nemocnice A bývá úspěšnější než v nemocnici B. Pacienty po operaci sledujeme po zvolený čas a zaznamenáme, zda došlo nebo nedošlo k výskytu komplikací. Souhrnně lze tyto údaje zapsat ve tvaru tzv. kontingenční tabulky, jejíž příklad vidíme na obrázku.
| Nemocnice A | Nemocnice B | Celkem | |
| Komplikace | 10 | 15 | 25 |
| Bez komplikací | 45 | 30 | 75 |
| Celkem | 55 | 45 | 100 |
Tento typ úlohy řeší test s názvem Pearsonův chí-kvadrát test, který je založen na předpokladu, že pokud by úspěšnost chirurgů byla v obou nemocnicích stejná, bylo by procento pacientů bez komplikací stejné v každé z nemocnic, jako je v obou skupinách pacientů dohromady, tedy 75 procent. Pokud se relativní četnost pacientů bez komplikací v každé z nemocnic nebude příliš lišit od 75 procent, závěrem testu bude, že jsou nemocnice srovnatelné, pokud se lišit bude, dostáváme závěr, že chirurgové v jedné z nemocnic jsou úspěšnější.
Výstupem statistických programů je typicky hodnota chí-kvadrát statistiky, dosažená p-hodnota (p-value) testu (pokud je menší než zvolená pětiprocentní hladina, nulová hypotéza – že mezi skupinami není rozdíl a oba znaky, komplikace a vybraná nemocnice, jsou vzájemně nezávislé – se zamítá, v opačném případě nulovou hypotézu nezamítáme).
Další častou úlohou je porovnání průměrné hodnoty nějaké spojité proměnné (např. věku) mezi dvěma či více skupinami pacientů. Pro tyto účely používáme v případě dvou skupin studentův dvouvýběrový t-test, v případě více skupin jeho zobecnění s názvem jednofaktorová analýza rozptylu (one-way anova). Obě metody je vhodné doplnit o krabicové grafy s průměrnými hodnotami podle skupin, což statistické programy často dělají automaticky – představa o rozdílu mezi skupinami je tak názornější.
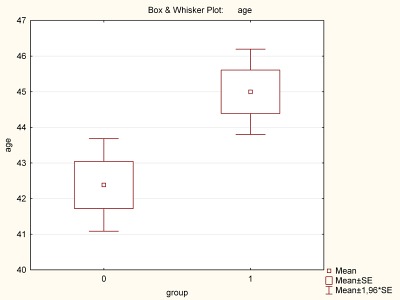
Obr. 1
Obr. 2
Ilustrační obrázek (obr. 1) ukazuje, že ve skupině 0 je v průměru nižší věk než ve skupině 1 (dosažený průměrný věk je 42,4, respektive 45 let). Rozdíl byl shledán statisticky významný (dosažená p-hodnota testu p=0,0038 je menší než pět procent). Je ale tento rozdíl i prakticky významný? Praktickou významnost zpravidla hodnotíme sestrojením 95procentního intervalu spolehlivosti pro rozdíl obou průměrných hodnot. Je-li tento interval úzký, máme poměrně jasnou představu o tom, jaký je pravděpodobný rozdíl mezi průměrným věkem obou skupin v rámci celé populace, pokud bude široký, může být rozdíl jak docela malý, tak poměrně vysoký. V uvedeném příkladě je 95procentní pravděpodobnost, že pacienti ve skupině 0 jsou v průměru nejméně o deset měsíců a nejvýše o čtyři a čtvrt roku mladší než pacienti ve skupině 1.
Samozřejmostí je pro dnešní softwary také ověření předpokladů těchto metod (již dříve zmíněné normální rozdělení hodnot sledované proměnné a také přibližně stejný rozptyl těchto hodnot ve skupinách), pokud program vyhodnotí předpoklady jako nesplněné, využívá se místo uvedených metod jejich neparametrických alternativ (Mann-Whitneyův test či Kruskal-Wallisova analýza rozptylu). Jelikož se jedná o nejčastěji používané metody, jsou i tyto neparametrické postupy součástí základních statistických balíků, někdy se mohou názvy testů lišit, ale vždy jsou k dispozici.
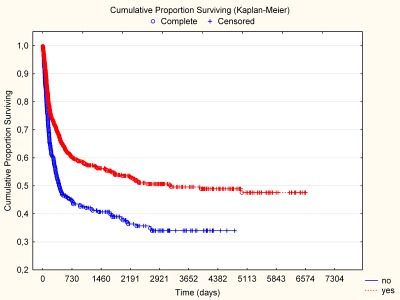
Poslední lékařskou analýzou, kterou bychom rádi zmínili, je analýza přežití (survival analysis). Pro tento typ analýzy je zpravidla třeba využít specializovaný statistický balíček, protože pracujeme s cenzorovanými daty. Pacienty sledujeme po určitou dobu, například pět let po operaci, a zajímá nás jejich přežití. Pokud pacient zemře, zaznamenáme čas jeho úmrtí (od doby po operaci) a to, že pacient zemřel. Pokud pacient nezemřel, zaznamenáme čas, kdy jsme ho přestali sledovat (maximálně tedy pět let), a informaci, že v zaznamenaném čase šlo o žijícího pacienta. Abychom pro analýzu využili maximum informace uložené v datech, je třeba využít záznamy jak žijících, tak zemřelých pacientů. To vyžaduje speciální metody. Nejčastěji volený přístup pro grafické znázornění je Kaplan-Meierova křivka, pro statistické porovnání přežití u dvou či více skupin pacientů je pak vhodná varianta log rankového testu.
Seřadíme-li podle velikosti časy, v nichž došlo podle našich záznamů k úmrtí pacientů, poskytuje Kaplan-Meierova křivka pro tyto doby pravděpodobnost, že pacient, který přežil některý z těchto časových okamžiků, nezemře ani v okamžiku bezprostředně následujícím. Na grafu vidíme porovnání dvou křivek přežití. Na první pohled je zřejmé, že z hlediska dlouhodobého přežití je na tom lépe skupina pacientů, jíž odpovídá červená křivka přežití.
Lékaři a statistika
Je patrné, že lékaři se neobejdou bez dobré databáze a statistického programu, který pokryje metody a grafická schémata odpovídající typům prováděných analýz. I když třeba nebudou lékaři provádět všechny analýzy sami, je dobré, aby byli schopni na nějaké základní úrovni zvolený statistický program používat, aby zvládli úpravu tabulek a grafů a některé jednoduché rutinní analýzy. Často je třeba také pomoci statistického odborníka. Málokterý lékař má totiž i odpovídající statistické vzdělání na takové úrovni, aby si poradil s nestandardními případy dat, nedostatkem pozorování a atypickými problémy, jimiž se praxe jen hemží. Ke spolupráci je třeba vybírat pečlivě takové odborníky, kteří mají zkušenost s daty z lékařských oborů. Velice často je totiž kamenem úrazu, že statistik-matematik a lékař naráží na obrovské potíže, když se snaží jeden druhému vysvětlit svůj pohled, potřeby a očekávání vkládané do spolupráce.
 |
Lenka Posch Autorka je konzultantkou a analytičkou firmy StatSoft. |


| Po | Út | St | Čt | Pá | So | Ne |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Formulář pro přidání akce















