- Přehledy IS
- APS (20)
- BPM - procesní řízení (23)
- Cloud computing (IaaS) (10)
- Cloud computing (SaaS) (33)
- CRM (51)
- DMS/ECM - správa dokumentů (20)
- EAM (17)
- Ekonomické systémy (68)
- ERP (77)
- HRM (28)
- ITSM (6)
- MES (32)
- Řízení výroby (36)
- WMS (29)
- Dodavatelé IT služeb a řešení
- Datová centra (25)
- Dodavatelé CAD/CAM/PLM/BIM... (39)
- Dodavatelé CRM (33)
- Dodavatelé DW-BI (50)
- Dodavatelé ERP (71)
- Informační bezpečnost (50)
- IT řešení pro logistiku (45)
- IT řešení pro stavebnictví (26)
- Řešení pro veřejný a státní sektor (27)
 ERP systémy
ERP systémy CRM systémy
CRM systémy Plánování a řízení výroby
Plánování a řízení výroby AI a Business Intelligence
AI a Business Intelligence DMS/ECM - Správa dokumentů
DMS/ECM - Správa dokumentů HRM/HCM - Řízení lidských zdrojů
HRM/HCM - Řízení lidských zdrojů EAM/CMMS - Správa majetku a údržby
EAM/CMMS - Správa majetku a údržby Účetní a ekonomické systémy
Účetní a ekonomické systémy ITSM (ITIL) - Řízení IT
ITSM (ITIL) - Řízení IT Cloud a virtualizace IT
Cloud a virtualizace IT IT Security
IT Security Logistika, řízení skladů, WMS
Logistika, řízení skladů, WMS IT právo
IT právo GIS - geografické informační systémy
GIS - geografické informační systémy Projektové řízení
Projektové řízení Trendy ICT
Trendy ICT E-commerce B2B/B2C
E-commerce B2B/B2C CAD/CAM/CAE/PLM/3D tisk
CAD/CAM/CAE/PLM/3D tisk | Přihlaste se k odběru zpravodaje SystemNEWS na LinkedIn, který každý týden přináší výběr článků z oblasti podnikové informatiky | |

| ||
Matematické metody v projektovém managementu
 Schopnost predikce doby trvání projektů a hodnoty práce, potažmo odpovídajících nákladů, je klíčovým úkolem současného projektového řízení. Především u projektů dodávaných do komerční sféry představuje řízení těchto rovin alfu a omegu úspěchu. Zejména časová zpoždění spojená s odloženým uvedením výstupu projektu na trh mají fatální dopady na celkový výnos, který vám z uplatnění výstupu na trhu plyne. Jinými slovy, pokud přijdete na trh pozdě, může se stát, že vás předběhne konkurence. Ono krátké období, kdy si můžete diktovat cenu, je tak pryč. Jak tedy lépe řídit časovou dimenzi projektů a ochránit se před těmito dopady?
Schopnost predikce doby trvání projektů a hodnoty práce, potažmo odpovídajících nákladů, je klíčovým úkolem současného projektového řízení. Především u projektů dodávaných do komerční sféry představuje řízení těchto rovin alfu a omegu úspěchu. Zejména časová zpoždění spojená s odloženým uvedením výstupu projektu na trh mají fatální dopady na celkový výnos, který vám z uplatnění výstupu na trhu plyne. Jinými slovy, pokud přijdete na trh pozdě, může se stát, že vás předběhne konkurence. Ono krátké období, kdy si můžete diktovat cenu, je tak pryč. Jak tedy lépe řídit časovou dimenzi projektů a ochránit se před těmito dopady?


V době komplexních projektů, paralelních úkolů a pohyblivých kritických cest je aplikace standardních metod, které nezahrnují variabilitu možných scénářů (např. PERT), nedostačující, a proto se moderní metodika predikce doby trvání projektů opírá o matematický aparát pravděpodobnostních (stochastických) výpočtů, který iterativně aplikuje v řádech sto- a tisícinásobků na možný vývoj projektu.
Matematické metody v projektovém managementu
V prostředí, v němž se dnes realizují projekty, se setkáte s trendem stále se zvyšujícího tlaku na efektivitu využití zdrojů, tedy snahu realizovat projekty s minimem zdrojů v co nejkratším možném čase. Dalo by se říci, že se tímto dnešní projekty v podstatě neliší od projektů realizovaných v minulosti. Zásadní změna je ovšem skryta hlouběji a spočívá v detailnějším plánování v důsledku aplikace stále sofistikovanějších informačních technologií na vedení nejen projektů, ale také většiny pracovních, dokonce i soukromých činností. Jsou to právě informační technologie atomizující náš čas, které nám také dávají nástroj, s jehož pomocí můžeme na jedné straně lépe plánovat projekty, například využitím softwaru pro projektové řízení, na druhé straně nám dávají výpočetní kapacitu k pokročilým matematickým výpočtům a otevírají tím cestu pro nové metody plánování.
Z pohledu projektového řízení je klíčové naplánovat projekt co nejefektivněji s ohledem na projektové zadání, které se ve většině případů váže jak na časovou, tak nákladovou rovinu. To znamená, že znalost metodiky odhadování hodnoty práce úkolů a určení doby trvání projektu má přímý dopad na celkovou efektivitu. Pokud byste se spoléhali nadále jen na standardní postupy plánování, tedy odhad pracnosti jednotlivých úkolů, vytvoření vazeb mezi úkoly a definování kritické cesty, pak sestavíte projektový plán, o němž se dá s určitostí tvrdit, že nebude dodržen. Důvodem je, že každý dílčí úkol projektu má jistou vlastní pravděpodobnost, se kterou bude či nebude v plánovaném čase hotov. Tato pravděpodobnost se umocňuje vazbami mezi úkoly, z nichž každý má svou vlastní pravděpodobnost dodržení plánovaného času.
Přestavte si, že máte za úkol sestavit plán školení pro implementaci nové verze softwaru na účetním oddělení vaší společnosti. Jedná se o menší projekt, jehož odhadovaná doba trvání je necelých padesát dnů (obr. 1). Jedním z úkolů, který není na kritické cestě, je zajistit školicí místnost. Tomuto úkolu předchází identifikace lektorů a té zas úkol sestavení harmonogramu školení. Pokud vezmete pro příklad, že každý úkol má padesátiprocentní pravděpodobnost dokončení dle plánu, pak zjistíte, že dokončení úkolu školicí místnost bude jen s 12,5% (0,53 = 12,5 %) pravděpodobností zajištěna včas.
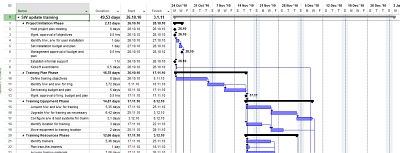
Obr. 1: Harmonogram projektu v aplikaci MS Project
Jak je z výše uvedeného patrné, tak vám v reálné situaci metoda kritické cesty nestačí k určení doby trvání projektu, ani pokud byste jednotlivé úkoly zpřesnily v odhadech další tradiční metodou, například PERT (z angl. Program Evaluation and Review Technique). Hlavním důvodem je absence komplexního přístupu, který by zahrnoval možnosti posunů v době trvání všech úkolů, čímž by došlo k sestavení nové kritické cesty, jejichž pravděpodobnosti by byla vyčíslena.
Absence aparátu pravděpodobnostních (stochastických) výpočtů však byla koncem minulého století vyřešena. Metoda takovýchto výpočtů byla sice již delší dobu známa, ale uvedení do širší praxe bránila hlavně výpočetní kapacita, kterou obdobný nástroj potřebuje k tomu, abyste mohli modelovat možné scénáře projektů na počkání.
Principy fungování metody Monte Carlo
Abyste tedy byli schopni lépe a přesněji predikovat vývoj chaosu zvaného projekt, můžete se opřít o metodu Monte Carlo, která nachází v poslední době čím dál širší uplatnění v prostředí projektového řízení. Autorem této metody je Stanislaw Ulam, americký matematik polského původu, který ji objevil v rámci výzkumu termonukleárních zbraní v rámci Manhattanského projektu. Tato fyzikální metoda se dnes používá pro řešení širokého spektra agend: například k výpočtu pravděpodobnosti výskytu částic v prostoru, v prognóze rizik finančních investic apod. Odsud se pak rozšířila na další společenskovědní odvětví, tedy i do projektového managementu.
Byť se na první pohled může zdát, že takovýto postup má pramálo společného s principy fungování projektu. Opak je pravdou, podíváte-li se na projekt jako na množinu úkolů, které se mohou společně ovlivňovat a kde má každý úkol vlastní pravděpodobnost, s jakou se jej podaří v daném čase dokončit. V tomto ohledu aplikace metody Monte Carlo do projektového řízení v principu spočívá v přiřazení proměnné zasazené do systému náhodných čísel v rozptylu rovnajícímu se rozptylu odhadů k danému úkolu. Pokud se například snažíte určit rozptyl neurčitosti doby trvání úkolu (např. Gaussovou křivkou), určíme si mantinely pesimistických a optimistických hodnot odhadu (jako u metody PERT).
Tento krok učiníme pro každý jednotlivý úkol projektu, nebo alespoň v minimalistické verzi pro každý souhrnný úkol projektu. Výsledkem jsou hodnoty, na které je následně aplikována deterministická analýza. Tento proces je opakován několiksetkrát, popřípadě několiktisíckrát (proto již zmíněná náročnost na výpočetní kapacitu), aby se došlo ke statisticky vypovídajícímu souhrnu dat. Takto vám opakovaná aplikace deterministické analýzy vygeneruje data s dostatečnou výpovědní hodnotou pro sestavení například S-křivky, z níž můžete vyčíst pravděpodobnost dokončení termínu projektu v požadovaném čase (obr. 2).
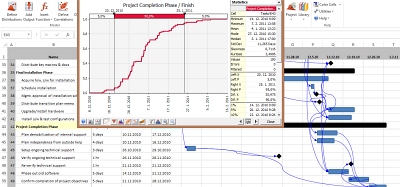
Obr. 2: Kalkulace doby trvání metodou Monte Carlo v aplikaci MS Excel pomocí doplňku @Risk. Zatímco podle metody kritické cesty by ilustrativní projekt měl skončit 3. ledna (viz obrázek 1), podíváte-li se na S-křivku, která je výsledkem Monte Carlo analýzy, vidíte, že s 90% pravděpodobností skončíte projekt v rozmezí 19.–26. ledna, přičemž termín dokončení mající pravděpodobnost vyšší než 95 procent je termín po 26. lednu (viz poslední sekce S-křivky s hlavičkou 5 %).
Pokud byste tedy jakožto projektový manažer uvedeného projektu včas provedli tuto analýzu, s největší pravděpodobností byste svůj projekt zahájili dříve, abyste stihli požadovaný termín dodání projektu, případně byste na základě tohoto modelu nastartovali jednání o posunu projektu zhruba o tři týdny. Důležitým prvkem je, že pro tuto diskusi máte v ruce číselný podklad, jehož absence zpravidla prosazení těchto změn hodně natahuje.
Z výše zmíněného je tedy patrné, že aplikace základních projektových metod, jakou jsou kritická cesta, PERT atd., trpí základním nedostatkem a také to, že nezohledňují do své metody dostatečně dynamičnost vývoje projektu, v důsledku čehož má výsledný termín získaný z těchto metod pouze nízkou pravděpodobnost úspěchu.
Kvantový management na obzoru
Vzorový případ je zvolen pro názornou jednoduchou ilustraci. Přesto když už malý projekt může mít takto „nečekaný“ vývoj, představte si, co může nastat u projektů v řádech větších, kde je více úkolů, více vazeb, a tedy více rizik. To je důvodem, proč některé společnosti začínají vyžadovat analýzu Monte Carlo jako podklad pro schválení před realizací projektů určité velikosti nebo u projektů, jejichž výsledkem má být nový produkt postavený na nových technologiích.
Projekty jsou a budou vždy rizikovou investicí, u níž již dávno nestačí mít na rizika připravené jen rezervy (u zmíněného přikladu by vám ostatně ani dvacetiprocentní termínová rezerva zdaleka nestačila). Naopak trendem dnešní doby je redukce rozsahu rezerv, což nevyhnutelně znamená zvýšit kvalitu plánování. Samozřejmě, že v konečném důsledku je i ta nejsofistikovanější metoda stále jen nástrojem a i nadále je to kvalita našich vstupních dat, která ovlivňuje výsledný výpočet. Nicméně samotné metody urazily pořádný kus cesty a s nadsázkou lze na závěr dodat, že je to právě pravděpodobnost spojující dnešní fyziku a management. V současnosti se totiž zpravidla v managementu spíše než o tom, jak se věci mají, diskutuje o tom, co se stane a s jakou pravděpodobností. Jinými slovy: vítejte v kvantovém managementu.
Drahoslav Dvořák, Daniel Lichtenberg Lisý
Daniel Lichtenberg Lisý je senior EPM consultant ve společnosti WBI Systems. Více jak deset let pracoval v oblasti vedení projektů. Je certifikovaným manažerem kvality.


| Po | Út | St | Čt | Pá | So | Ne |
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 | 1 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 12.2. | Kontejnery v praxi 2026 |
| 26.2. | IT ve zdravotnictví 2026 |
| 12.3. | IT Security Worshop 2026 |
| 15.4. | Energy Vision 2026 |
| 12.5. | Cloud Computing Conference 2026 |
Formulář pro přidání akce














