- Přehledy IS
- APS (20)
- BPM - procesní řízení (22)
- Cloud computing (IaaS) (10)
- Cloud computing (SaaS) (33)
- CRM (51)
- DMS/ECM - správa dokumentů (20)
- EAM (17)
- Ekonomické systémy (68)
- ERP (79)
- HRM (28)
- ITSM (6)
- MES (32)
- Řízení výroby (36)
- WMS (29)
- Dodavatelé IT služeb a řešení
- Datová centra (25)
- Dodavatelé CAD/CAM/PLM/BIM... (39)
- Dodavatelé CRM (33)
- Dodavatelé DW-BI (50)
- Dodavatelé ERP (71)
- Informační bezpečnost (50)
- IT řešení pro logistiku (45)
- IT řešení pro stavebnictví (26)
- Řešení pro veřejný a státní sektor (27)
 ERP systémy
ERP systémy CRM systémy
CRM systémy Plánování a řízení výroby
Plánování a řízení výroby AI a Business Intelligence
AI a Business Intelligence DMS/ECM - Správa dokumentů
DMS/ECM - Správa dokumentů HRM/HCM - Řízení lidských zdrojů
HRM/HCM - Řízení lidských zdrojů EAM/CMMS - Správa majetku a údržby
EAM/CMMS - Správa majetku a údržby Účetní a ekonomické systémy
Účetní a ekonomické systémy ITSM (ITIL) - Řízení IT
ITSM (ITIL) - Řízení IT Cloud a virtualizace IT
Cloud a virtualizace IT IT Security
IT Security Logistika, řízení skladů, WMS
Logistika, řízení skladů, WMS IT právo
IT právo GIS - geografické informační systémy
GIS - geografické informační systémy Projektové řízení
Projektové řízení Trendy ICT
Trendy ICT E-commerce B2B/B2C
E-commerce B2B/B2C CAD/CAM/CAE/PLM/3D tisk
CAD/CAM/CAE/PLM/3D tisk| Přihlaste se k odběru newsletteru SystemNEWS, který každý týden přináší výběr článků z oblasti podnikové informatiky | |
 | |
Neuronové sítě a jejich využití
 Klasifikace podvodného pojistného plnění pomocí neuronové sítě? Ano, proč ne, jde o jednu z nejúčinnějších klasifikačních metod. Vzhledem k vzrůstající popularitě neuronových sítí jsme se rozhodli vám je v tomto článku představit a říci si něco o jejich využití.
Klasifikace podvodného pojistného plnění pomocí neuronové sítě? Ano, proč ne, jde o jednu z nejúčinnějších klasifikačních metod. Vzhledem k vzrůstající popularitě neuronových sítí jsme se rozhodli vám je v tomto článku představit a říci si něco o jejich využití.


Neuronová síť
Neuronová síť je algoritmus, který si bere za vzor činnost lidského mozku. Je to metoda, která spadá do tzv. data miningu. Již v dřívějších dobách bylo zjištěno, že mozek je tvořen velkým množstvím vzájemně propletených buněk, které nazýváme neurony, jež spolu komunikují pomocí elektrických impulzů. Od vzniku prvních počítačů se programátorské kapacity snaží vytvořit algoritmus, který bude činnost lidského mozku napodobovat. Vzniká tak pojem umělá inteligence, který výsledky takového snažení někdy více a někdy méně reprezentuje. Princip neuronových sítí je v dnešní době implementován v řadě dostupných analytických a rozhodovacích softwarů a v různých oborech lidské činnosti podává extrémně dobré výsledky, tedy ve srovnání se „standardními“ typy rozhodovacích algoritmů.
Princip sítě
Princip softwarové neuronové sítě, jak už bylo řečeno a je odhadnutelné z názvu, se inspiruje biologickou neuronovou sítí, kde je základním stavebním kamenem (zjednodušeně řečeno) nervová buňka – neuron. Jednotlivé neurony jsou vzájemně propojeny spoji ohodnocenými vahami. Takovéto propojení a schopnost tyto váhy adaptovat (učit se) na základě trénovacích vzorů v datech dává neuronové síti nové široké možnosti v oblasti analýzy dat.
Hlavní předností neuronové sítě je schopnost učit se, tedy zapamatovat si kombinace, které vedly k požadovanému výstupu, a u nových vstupů se potom obracet na „svou“ paměť a na základě zkušeností odhadovat nový výsledek. V tomto případě mluvíme o generalizaci (zevšeobecňování), která je další velkou předností algoritmu neuronových sítí. Zjednodušeně řečeno, jde o přiměřenou dovednost správně zareagovat i na vstupy, které nebyly součástí trénovacích dat, a vyvodit z nich obecné závěry o datech. Schopnost učit se bývá někdy dokonce považována za definici umělé inteligence.
Často v praxi nemáme ani dostatek apriorních znalostí o tom, co způsobuje konkrétní variabilitu zkoumané proměnné, a není proto jiná možnost, než se vlivy snažit popsat na základě historický naměřených dat. Učení se z historických dat je dnes součástí mnoha oborů, včetně data miningu, do kterého v našem pojetí neuronové sítě řadíme.
Další vlastností neuronových sítí je schopnost řešit i silně nelineární úlohy. Využití neuronové sítě v analýze dat má smysl všude tam, kde selhávají „klasické“ modely, jako například regrese. V některých případech se stává, že není možné najít nějakou jednoduchou matematickou funkci, která by vhodně postihla všechny vlivy, které variabilitu sledované proměnné ovlivňují. Potom jsou neuronové sítě vhodná alternativa. Neuronové sítě jsou také do jisté míry schopné pracovat s nepřesnými daty a šumy. My však doporučujeme provést vždy čištění a přípravu dat.
Možností aplikace neuronových sítí je celá řada, dají se využít na následující typy úloh:
- Regrese – regresní analýza se zabývá předpovídáním spojité proměnné na základě vstupů (spojitých či kategorických prediktorů – nezávislých proměnných).
- Klasifikace – neboli zařazování do tříd. Na základě úrovně cílové proměnné a kombinace vstupů, které ke konkrétnímu výsledku vedou, bude vytvořen model, který dokáže klasifikovat nová data. Typickým příkladem jsou bankovní problémy, které řeší otázky bonity klienta, schopnost jeho splácení, ale také problémy typu poslat či neposlat pacienta na podrobné vyšetření, detekce spamu apod.
- Časové řady (regrese) – slouží k modelování spojitých proměnných, které prochází vývojem v čase, respektive časových řad. V této situaci můžeme vybrat buď pouze jedinou závislou proměnnou, kde model bude vycházet ze zpožděných hodnot této časové řady, nebo máme možnost zvolit další proměnné, které budou tuto řadu vysvětlovat.
- Časové řady (klasifikace) – tento typ analýzy použijeme tehdy, je-li naše cílová (závislá) proměnná kategorické povahy. Závislou proměnnou lze vysvětlovat opět pouze svým „historickým“ průběhem v čase, případně je možné zvolit další spojité i kategorické prediktory jako nezávislé vysvětlující proměnné.
- Shluková analýza – tento typ analýzy nepoužívá závislou proměnnou (učení bez učitele), cílem je detekovat netriviální shluky v datech. Jde o tzv. Kohonenovu síť. Vstupem jsou pouze hodnoty (vstupních) nezávislých proměnných. Kohonenovu síť (též self-organizing feature map – SOFM) chápejme jako druh shlukové analýzy (vektorovou kvantizaci).
Poznamenejme, že máme také možnost zvolit více závislých proměnných pro analýzu. Což znamená například možnost modelovat vícerozměrnou časovou řadu.
Model neuronu
Jak již bylo naznačeno, neuronové sítě se skládají z neuronů propojených vazbami. Model neuronu se skládá ze tří částí: vstupní, výstupní a funkční. Na základě vah mohou být jednotlivé vstupy potlačeny, nebo naopak zvýhodněny. Jeden neuron sám o sobě není schopen vykonávat o nic moc složitější funkci než klasická regresní analýza. Síla neuronové sítě se však projeví až při propojení neuronů mezi sebou do větších struktur. Neurony jsou uspořádány do vrstev. Nezapomeňme, že algoritmus se učí sám a všechny váhy si sám volí. Pokud si představíme, jak takovouto sítí proudí příchozí data, je nám jasné, že právě díky složitosti spojení dokáže neuronová síť najít i složitější a nelineární vztahy, na druhou stranu je ale pravda, že ze získané neuronové sítě nikdy nebudeme schopni získat interpretaci, proč to u konkrétního pozorování dopadlo, jak to dopadlo. Je to tedy metoda typu „black box“ – nejsme schopni jednoduše interpretovat výsledky či získat jednoduchý předpis závislosti mezi závislou a nezávislými proměnnými. Tato vlastnost nám vůbec nevadí, pokud nám jde pouze o předpověď veličiny v oblasti našeho zájmů, nicméně pokud chceme zjistit i důvody výsledku, pak nám tato metoda příliš nepomůže. Nejpoužívanější typy neuronových sítí jsou: vícevrstvá perceptronová síť, radial basis function, Kohonenova síť, lineární síť a Bayesovské sítě. Každý typ sítě má různé vlastnosti, výběr závisí na povaze úlohy a charakteru dat.
Hrozba přeučení sítě
Obecně platí, že pokud síť obsahuje malý počet neuronů, její schopnost vystihnout a popsat závislosti v trénovacích datech je slabší. Pokud bude síť naopak obsahovat příliš velký počet neuronů, tato síť pravděpodobně nebude mít problém navést a reprezentovat závislosti v trénovacích datech, ale její schopnost generalizace, tedy vystihnout správný výsledek na nových datech, může být horší. Takovému jevu se říká přeučení sítě (overfitting). K přeučení také může docházet ve chvíli, kdy model obsahuje velký počet vstupních parametrů a relativně málo pozorování. Cílem tedy není maximalizace výkonu sítě na trénovacích datech, ale rozumný kompromis mezi trénovacím výkonem a schopností zevšeobecňovat znalosti i na nových datech. S tím, o čem zde píšeme, úzce souvisí následující princip rozdělení datového souboru, který neuronové sítě implicitně používají. Jedná se o rozdělení dat na trénovací, testovací, případně validační množinu:
- trénovací množina – náhodně vybraná část dat, která slouží pro učení sítě,
- testovací množina – další část dat sloužící k zastavení trénovaní, aby nedošlo k přeučení sítě,
- validační množina – zbytek dat, na kterém ověříme konečnou kvalitu modelu – jde o data, která dosud model k dispozici neměl.
Typicky se toto rozdělení dělá v poměru 50/25/25, případně 70/15/15. Ve výsledcích je pak reportován výkon na každé z těchto množin, přičemž většinou vybíráme model, který nemá příliš velké výkyvy mezi výkony na jednotlivých množinách.
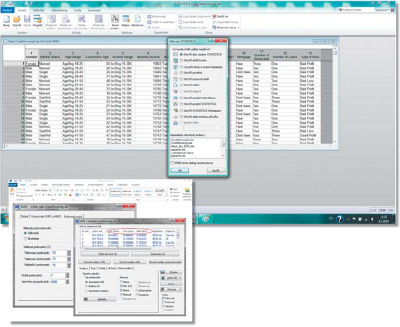
Obr. 1: Dialog pro výběr poměru vzorků a dialog výsledných sítí (zdroj: Archiv StatSoft)
Využití neuronových sítí
Neuronové sítě mají (někdy až pozoruhodnou) schopnost extrahovat pravidla a trendy z komplikovaných průběhů v datech. Další vlastností je, při správné aplikaci, schopnost velmi přesně předpovědět údaje, které nebyly součástí trénovacích dat, tedy schopnost zobecňovat. Tuto schopnost mají samozřejmě i jiné typy algoritmů, které spadají do data miningu. Neuronové sítě se nejčastěji používají například v následujících oblastech:
- reakce spotřebitelů na nové zboží,
- detekce úvěrového rizika,
- detekce pojistného podvodu,
- odhad dynamické stability u energetických systémů,
- rozpoznání poruch strojů a výpočetní techniky,
- lékařství – detekce a odhad velikosti tumoru, chemická diagnostika,
- dopravní signalizace,
- rozpoznání kvality výrobku bez nutnosti laboratorních experimentů,
- předpověď finančních časových řad včetně velmi dynamických řad (burza, směnné kurzy),
- samoobslužné mechanismy (subsystémy řízení budov),
- optické rozpoznávání textů, písma a podpisů,
- systémy pro převod mluvené řeči do písemné podoby,
- odhad kvality ropných produktů.
Miloš Uldrich, Tomáš Jurczyk
| 12.3. | IT Security Workshop 2026 |
| 19.3. | Jak dostat výrobu pod kontrolu aneb realistické plánování... |
| 25.3. | Konference SCADA SECURITY |
| 15.4. | Energy Vision 2026 |
| 12.5. | Cloud Computing Conference 2026 |
Formulář pro přidání akce
| 13.3. | CONTROLLING A BI PRAKTICKY - Manažerská výsledovka |

















