- Přehledy IS
- APS (20)
- BPM - procesní řízení (23)
- Cloud computing (IaaS) (10)
- Cloud computing (SaaS) (33)
- CRM (51)
- DMS/ECM - správa dokumentů (20)
- EAM (17)
- Ekonomické systémy (68)
- ERP (78)
- HRM (28)
- ITSM (6)
- MES (32)
- Řízení výroby (36)
- WMS (29)
- Dodavatelé IT služeb a řešení
- Datová centra (25)
- Dodavatelé CAD/CAM/PLM/BIM... (39)
- Dodavatelé CRM (33)
- Dodavatelé DW-BI (50)
- Dodavatelé ERP (71)
- Informační bezpečnost (50)
- IT řešení pro logistiku (45)
- IT řešení pro stavebnictví (26)
- Řešení pro veřejný a státní sektor (27)
 ERP systémy
ERP systémy CRM systémy
CRM systémy Plánování a řízení výroby
Plánování a řízení výroby AI a Business Intelligence
AI a Business Intelligence DMS/ECM - Správa dokumentů
DMS/ECM - Správa dokumentů HRM/HCM - Řízení lidských zdrojů
HRM/HCM - Řízení lidských zdrojů EAM/CMMS - Správa majetku a údržby
EAM/CMMS - Správa majetku a údržby Účetní a ekonomické systémy
Účetní a ekonomické systémy ITSM (ITIL) - Řízení IT
ITSM (ITIL) - Řízení IT Cloud a virtualizace IT
Cloud a virtualizace IT IT Security
IT Security Logistika, řízení skladů, WMS
Logistika, řízení skladů, WMS IT právo
IT právo GIS - geografické informační systémy
GIS - geografické informační systémy Projektové řízení
Projektové řízení Trendy ICT
Trendy ICT E-commerce B2B/B2C
E-commerce B2B/B2C CAD/CAM/CAE/PLM/3D tisk
CAD/CAM/CAE/PLM/3D tisk| Přihlaste se k odběru newsletteru SystemNEWS, který každý týden přináší výběr článků z oblasti podnikové informatiky | |
 | |
Explicitní řešič pro strukturální analýzy?
 Mechanika je klíčovou oblastí při řešení mnoha různých technických problémů, ať už se jedná o vývoj nových produktů, optimalizaci existujících systémů, nebo simulujeme chování při extrémních podmínkách. Pro řešení těchto problémů se nejběžněji používají implicitní řešiče, které jsou v lineární podobě často součástí i běžných CAD systémů. Tyto řešiče pracují na principu implicitního numerického řešení diferenciálních rovnic a jsou vynikající především pro řešení statických úloh. Vhodné jsou i pro řešení nelineárního chování kontaktů nebo materiálů.
Mechanika je klíčovou oblastí při řešení mnoha různých technických problémů, ať už se jedná o vývoj nových produktů, optimalizaci existujících systémů, nebo simulujeme chování při extrémních podmínkách. Pro řešení těchto problémů se nejběžněji používají implicitní řešiče, které jsou v lineární podobě často součástí i běžných CAD systémů. Tyto řešiče pracují na principu implicitního numerického řešení diferenciálních rovnic a jsou vynikající především pro řešení statických úloh. Vhodné jsou i pro řešení nelineárního chování kontaktů nebo materiálů.


Avšak implicitní řešiče mohou být někdy problematické kvůli své složitosti a náročnosti na výpočetní zdroje. Tyto řešiče vyžadují, především pro nelineární problémy, pečlivé nastavení vstupních parametrů a mohou mít tendenci při výpočtu nekonvergovat.
Na druhé straně, explicitní řešiče mechaniky fungují na principu explicitního numerického řešení diferenciálních rovnic v nichž se vyskytuje i časová složka a poskytují jednodušší a robustnější řešení. Tyto řešiče umožňují řešit problémy s vysokou rychlostí a přesností, aniž by bylo nutné nastavovat složité parametry výpočtu. Navíc jsou explicitní řešiče vhodné pro řešení problémů s rychlými změnami stavu, jako jsou například kolize a deformace.
Implicitní a explicitní řešiče mechaniky poskytují každý jiné výhody a nevýhody a hodí se k řešení jiných mechanických úloh. Proto je důležité před simulací zvážit použití obou typů řešičů, aby bylo možné dosáhnout co nejlepšího výsledku. Úvaha by měla brát v potaz specifické potřeby daného projektu a volba by měla být založena na kombinaci rychlosti, přesnosti a schopnosti řešit složité úlohy. Je důležité si uvědomit, že implicitní a explicitní řešiče nejsou vzájemně se vylučující, a mohou být k dosažení nejlepších výsledků použity i společně.
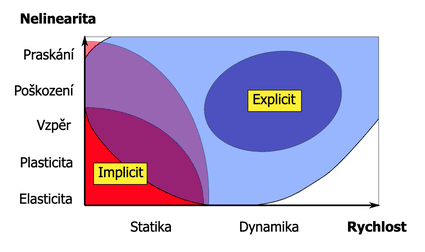
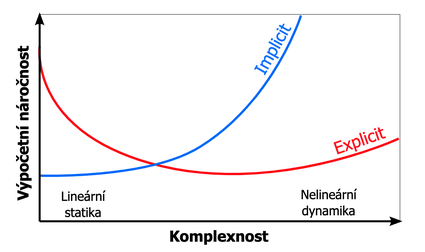
Výběr správného typu analýzy je někdy proveden nesprávně z důvodu nedostatečných znalostí o zkoumaném problému. Často se zvolí jednodušší řešení řešitele a zanedbá se složitost situace. Například se chybně zvolí lineární analýza, když problém vyžaduje úvahy o plasticitě.
Jaký řešič tedy kdy volit?
Nejprve je potřeba si uvědomit, zda je úloha časově závislá, či nezávislá. Pokud je vliv zrychlení v úloze významný a nelze jej zanedbat, označujeme problémy jako časově závislé. Například při pádové zkoušce, kdy se předmět zpomaluje až nadoraz, se největší síla projeví během prvních několika milisekund. V tomto případě je nutné zohlednit vliv takového zpomalení. Naproti tomu lze zatížení považovat za kvazistatické nebo časově nezávislé, pokud na konstrukci působí zatížení pomalu. Je-li rychlost zatěžování dostatečně pomalá, lze účinky zrychlení zanedbat.

Implicitní řešení je užitečné v problémech, kde časová závislost řešení není důležitým faktorem (jako je statická nebo modální analýza apod.), zatímco explicitní řešení je nejužitečnější při řešení problémů s vysokou závislostí deformace na čase (nárazy, pády, rázy a další).
Analýza explicitní dynamiky se používá ke stanovení dynamické odezvy konstrukce v důsledku šíření napěťové vlny, nárazu nebo rychle se měnícího časově závislého zatížení. Setrvačné účinky a předání hybnosti mezi pohybujícími se tělesy jsou obvykle důležitými aspekty tohoto typu analýzy. Lze ji použít také k modelování mechanických jevů, které jsou vysoce nelineární. Nelinearity mohou vycházet z materiálů, z kontaktů a z geometrické deformace.
Podíváme-li se na nelinearity detailněji, můžeme uvést jednotlivé příklady. Za nelineární chování materiálů považujeme hyperelasticitu, plastické toky a především poruchy. Chceme-li simulovat lámání, praskání materiálu a následné šíření trhlin, bez explicitního řešení se neobejdeme. V oblasti kontaktů je explicit nástrojem pro řešení vysokorychlostních srážek a nárazů. A nakonec představiteli geometrické nelinearity mohou být vzpěr nebo zborcení. Především u zborcení si s implicitním řešičem nevystačíme.
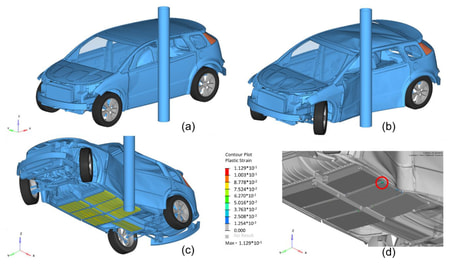
Typickými příklady explicitní analýzy v praxi jsou simulace nárazových zkoušek automobilů, simulace srážky letadla s ptákem, vyřazení lopatek proudového motoru, ale i běžnější úlohy jakými je třeba pádová zkouška využívaná u vývoje, elektroniky, dílenského nářadí nebo obalů.
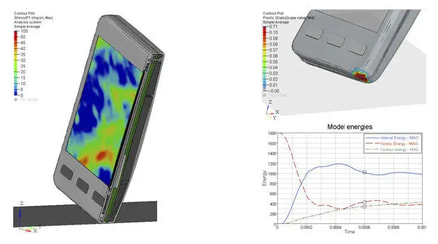
V automobilovém průmyslu nalezne explicitní řešič využití nejen u zmiňovaných crash-testů, ale i při vývoji plastových upevňovacích prvků (zácvaků), nebo dílčích prvků pasivní bezpečnosti (předepínače pásů, airbagy, zámky), u zkoušek mechanické odolnosti nabíjecích konektorů nebo baterií v elektromobilitě.
Z oblasti obranného průmyslu jmenujme simulace explozí nebo odolnosti proti střelám.
V systému Altair Radioss jsou k dispozici jak implicitní, tak explicitní schémata časové integrace. V explicitním schématu se rychlosti a posuny získávají přímou integrací uzlových zrychlení. Při tomto přístupu je časový krok cyklu často malý z důvodu stability. Proto je u statických nebo pomalých dynamických výpočtů, kde je doba trvání studie dlouhá, nutné k provedení simulace provést mnoho cyklů. Alternativou k explicitní metodě je v takových případech implicitní schéma časové integrace. Lze ukázat, že implicitní schéma je bezpodmínečně stabilní, což vede k většímu časovému kroku cyklu ve srovnání s explicitní metodou. V implicitním schématu je však třeba sestavit a invertovat globální matici tuhosti, což vede k vyšším paměťovým nárokům na jeden zatěžovací krok. Ačkoli je implicitní schéma bezpodmínečně stabilní, není bezpodmínečně konvergovatelné (nelineární případ). Ve skutečnosti je obecně méně robustní než explicitní schéma a vyžaduje větší zapojení uživatele. Rovnováha je vynucována parametry tolerancí stanovených uživatelem. Implicitní analýza si lépe poradí s problémy, jakými jsou cyklické zatížení, průraz a zpětný ráz.
Explicitní přístup je vhodnější pro rychlé dynamické problémy s vysoce nelineárním geometrickým a materiálovým chováním. Protože se všemi veličinami lze zacházet jako s vektory, je zapotřebí málo paměti. Explicitní dynamické řešiče poskytují alternativní přístup k řešení vysoce nelineárních statických analýz, které nekonvergují nebo konvergují s implicitním řešitelem velmi pomalu. Modely, které zahrnují složité kontakty s výrazným posuvem a vysoce nelineárním chováním materiálu a deformací prvků, lze zvládnout pomocí explicitních řešičů. Zatímco implicitní řešiče jsou pro statické problémy stále první volbou, explicitní řešiče s vhodným nastavením přechodového času a tlumení lze použít k zajištění robustních řešení obzvláště problematických statických problémů.
Zvažte tedy, zda si při simulacích i nadále vystačíte s běžným implicitním řešičem, nebo je načase implementovat do vývojového procesu i simulace založené na explicitním řešení.
Autor článku je Project Engineer ve společnosti Advanced Engineering s.r.o.


| 12.2. | Kontejnery v praxi 2026 |
| 26.2. | IT ve zdravotnictví 2026 |
| 12.3. | IT Security Worshop 2026 |
| 19.3. | Jak dostat výrobu pod kontrolu aneb realistické plánování... |
| 15.4. | Energy Vision 2026 |
Formulář pro přidání akce
| 18.2. | Webinář: AI pro firemní procesy: bezpečnost na prvním... |
| 26.2. | Kyberbezpečnost v IT bez strašení: kde začít? |














