- Přehledy IS
- APS (20)
- BPM - procesní řízení (22)
- Cloud computing (IaaS) (10)
- Cloud computing (SaaS) (33)
- CRM (51)
- DMS/ECM - správa dokumentů (20)
- EAM (17)
- Ekonomické systémy (68)
- ERP (78)
- HRM (28)
- ITSM (6)
- MES (32)
- Řízení výroby (36)
- WMS (29)
- Dodavatelé IT služeb a řešení
- Datová centra (25)
- Dodavatelé CAD/CAM/PLM/BIM... (39)
- Dodavatelé CRM (33)
- Dodavatelé DW-BI (50)
- Dodavatelé ERP (71)
- Informační bezpečnost (50)
- IT řešení pro logistiku (45)
- IT řešení pro stavebnictví (26)
- Řešení pro veřejný a státní sektor (27)
 ERP systémy
ERP systémy CRM systémy
CRM systémy Plánování a řízení výroby
Plánování a řízení výroby AI a Business Intelligence
AI a Business Intelligence DMS/ECM - Správa dokumentů
DMS/ECM - Správa dokumentů HRM/HCM - Řízení lidských zdrojů
HRM/HCM - Řízení lidských zdrojů EAM/CMMS - Správa majetku a údržby
EAM/CMMS - Správa majetku a údržby Účetní a ekonomické systémy
Účetní a ekonomické systémy ITSM (ITIL) - Řízení IT
ITSM (ITIL) - Řízení IT Cloud a virtualizace IT
Cloud a virtualizace IT IT Security
IT Security Logistika, řízení skladů, WMS
Logistika, řízení skladů, WMS IT právo
IT právo GIS - geografické informační systémy
GIS - geografické informační systémy Projektové řízení
Projektové řízení Trendy ICT
Trendy ICT E-commerce B2B/B2C
E-commerce B2B/B2C CAD/CAM/CAE/PLM/3D tisk
CAD/CAM/CAE/PLM/3D tisk| Přihlaste se k odběru newsletteru SystemNEWS, který každý týden přináší výběr článků z oblasti podnikové informatiky | |
 | |
Optimalizace logistických procesů a materiálových toků
 Jedním z dílčích cílů řady podniků je v současnosti optimalizace vnitropodnikových procesů. Ta se zpravidla zaměřuje na výrobní a logistické procesy, způsoby řízení výroby a nastavení materiálového toku, který souvisí se změnou layoutu, tedy vhodného rozmístění pracovišť. Navrhovaná opatření bývají v různých podnicích různě úspěšná. To je dáno především skutečností, že veškeré činnosti v podniku se vzájemně ovlivňují a často není možné dopředu predikovat, jaký bude výsledný dopad navrhovaných změn.
Jedním z dílčích cílů řady podniků je v současnosti optimalizace vnitropodnikových procesů. Ta se zpravidla zaměřuje na výrobní a logistické procesy, způsoby řízení výroby a nastavení materiálového toku, který souvisí se změnou layoutu, tedy vhodného rozmístění pracovišť. Navrhovaná opatření bývají v různých podnicích různě úspěšná. To je dáno především skutečností, že veškeré činnosti v podniku se vzájemně ovlivňují a často není možné dopředu predikovat, jaký bude výsledný dopad navrhovaných změn.


Jednou z možností, jak řádově zvýšit pravděpodobnost realizace správných rozhodnutí v podniku, je k podpoře rozhodování využít diskrétních simulačních modelů. Tato problematika již byla zmíněna v IT Systems 11/2013 v článku Simulace logistických toků a zásobování materiálem [1].
Počítačová simulace
Existuje celá řada definic simulace. Jednou z prvních a velmi výstižných definic je ta Dahlova, která vnímá simulaci jako výzkumnou metodu, „jejíž podstata spočívá v tom, že zkoumaný dynamický systém nahradíme jeho simulátorem (modelem) a s ním provádíme pokusy (experimenty) s cílem získat informaci o původním zkoumaném systému“ [2]. Simulace může být chápána jako napodobení operací procesů nebo systému reálného světa v toku času [3]. S její pomocí se generuje virtuální historie simulovaného systému. Tato historie pak vykresluje události, které by se uskutečnily v reálném systému.
Optimalizace
Poměrně problematická a často velmi časově náročná na výpočetní čas i výkonných počítačů je nutnost provedení mnoha simulačních experimentů v případě řešení rozsáhlejších simulačních úloh. Mnohdy je úloha vzhledem k vysokým nárokům na výpočetní čas prakticky neproveditelná. Například při řešení úlohy optimálního nastavení pěti parametrů, z nichž každý může nabýt jen deseti hodnot, bude třeba pro prohledání celého prostoru řešení celkem 105 experimentů, což by si například při trvání jednoho experimentu v délce jedné minuty vyžádalo výpočetní čas v délce zhruba sedmdesáti dní. Proto je vždy nezbytné usilovat o provedení co nejmenšího počtu simulačních experimentů při současném zachování přijatelné úrovně přesnosti výsledků. Pro tyto účely lze využít optimalizační nástroje, které jsou zpravidla součástí simulačních nástrojů.

Obr. 1
Princip fungování těchto optimalizačních metod lze demonstrovat například na jednoduché metodě označované jako algoritmus slepého horolezce. Celý princip tohoto algoritmu si můžeme představit následovně. Slepý horolezec si stoupne na náhodně zvolené počáteční místo a náhodně si vybere místa ve svém okolí, která ohodnotí z hlediska výšky. Přesune se na nejvyšší nové nalezené místo, z něhož opět hledá nové nejvyšší místo v daném okolí. Takto horolezec pokračuje, dokud nachází ve svém okolí vyšší bod, než na jakém se v současném okamžiku nalézá, přičemž je nutné reflektovat skutečnost, že nevidí do dálky, kde se nachází vrchol. Z obrázku 1 je patrné, že tato optimalizační metoda nezaručí nalezení nejvyššího vrcholu, jelikož může dojít k uvíznutí horolezce na jakémkoliv výčnělku. Toto platí obecně pro všechny optimalizační metody, které se tento problém uvíznutí snaží různým způsobem řešit. Optimalizační metody zpravidla nevedou k nalezení optimálního řešení, ale pouze řešení suboptimálního, které je však lepší než výchozí (současné) řešení.
Optimalizační metody pro řízení simulačních experimentů
Simulační model výrobního systému je virtuální, tj. je počítačovou podobou reálného (nebo zamýšleného) výrobního systému (tento model zaznamenává realitu více či méně detailně). Na simulačním modelu se „provádí“ zadaná virtuální výroba, která s určitou přesností imituje reálnou výrobu. Výstupy z jedné konkrétní virtuální výroby realizované jedním simulačním experimentem lze vyhodnotit jako jednu hodnotu kriteriální funkce F, jindy označované jako účelová nebo cílová funkce, u genetických algoritmů jako „fitness“. Hodnota F je funkcí vstupních hodnot do modelu označených vektorem X. Žádaná strategie provádění experimentů je taková, která co nejrychleji a nejpřesněji nalezne X, které má optimální hodnotu F (X) v zadaném oboru přípustných hodnot X. Tuto žádanou optimální hodnotu a její argument lze hledat pomocí tzv. optimalizačních metod (optimalizačních algoritmů). [4]
Cílem simulační optimalizace je nalézt takovou kombinaci hodnot n-faktorů X=(x1,x2,...,xn), pro kterou obdržíme optimální hodnotu jednoho z výstupů y(X), většinou však hodnotu „souhrnné“ kriteriální funkce F(X) – viz obrázek 2.
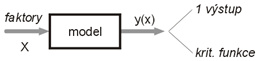
Obr. 2
V diskrétní simulaci jsou velice často používanými optimalizačními metodami genetické algoritmy. Tyto algoritmy jsou ve své podstatě jednoduchými modely Darwinovy evoluční teorie vývoje populací. Snahou je tedy napodobit přírodní výběr, v rámci něhož dochází k přežití silnějšího jedince, a tento výběr využít v oblasti optimalizace. Mírou přizpůsobení je tzv. fitness jedince. Jedinci s vyšší hodnotou fitness mají větší pravděpodobnost přežití a reprodukce svých genů do generace potomků. Kromě reprodukce se v populačním vývoji uplatňuje i tzv. mutace, což je náhodná změna genetické informace některých jedinců v populaci. [5]
Optimalizace logistických procesů a materiálových toků
Jak již bylo uvedeno, celkové chování výrobních systémů závisí na mnoha faktorech, které se vzájemně ovlivňují. Jedním z významných faktorů ovlivňujících celkovou výkonnost výrobního systému je vhodné nastavení logistických toků a zvolený způsob zásobování linek materiálem.
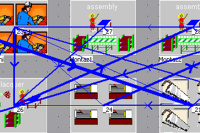
Na následujících dvou jednoduchých příkladech lze demonstrovat, jak je při hledání vhodného nastavení logistických procesů a materiálových toků možné využít optimalizační nástroje. Zatímco první příklad představuje možné způsoby optimálního nastavení trasy pro vláčky zavážející linky, druhý příklad demonstruje, jak z pohledu minimalizace délky přepravních cest optimálně rozmístit pracoviště vyrábějící několik různých výrobků.
Zavážení linek v pravidelných intervalech
Obrázek 3 ukazuje podnik, v němž je osm výrobních linek typu U, přičemž u každé linky jsou definována čtyři vykládací místa (celkem tedy 32 vykládacích míst). Zásobování linek ze skladu zajišťují vláčky maximálně se čtyřmi vagony, kdy každý vláček objíždí svojí vlastní trasu. Vláčky, které ze skladu k výrobním linkám dopravují dvě stě různých dílů, vyjíždějí ze skladu v pravidelných intervalech. V levé části obrázku je schéma výrobního podniku. V pravé části obrázku je zobrazen simulační model.
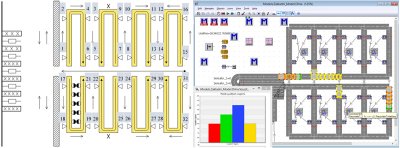
Obr. 3
U této studie budeme pomocí optimalizačního nástroje hledat:
- vhodný způsob nastavení dopravního systému tak, aby všechny linky byly včas zásobeny materiálem,
- optimální počet a sled vykládacích míst pro jednotlivé vláčky.
Nejdříve je nutné definovat účelovou funkci, která slouží k hodnocení vhodnosti nastavení zavážení linek. Cílem je minimalizace této účelové funkce.
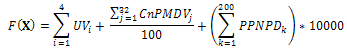
Obr. 2
kde:
- F(X) – výsledná účelová funkce
- UVi – ujetá vzdálenost i-tého vláčku [m]
- CnPMDVj – čas nad povolenou maximální dobu dodání dílu na j-té vykládací místo linky [s]
- PPNPDk – počet požadavků na dopravu k-tého dílu na linku, který nemá přiřazený vláček na dopravu
Ve funkci je sčítána celková ujetá vzdálenost vláčků s penalizací za včasné nedovezení dílů na jednotlivá vykládací místa a dále je přičteno penále za fyzické nedodání některých dílů na požadovanou linku. K optimalizaci byl v tomto případě použit genetický algoritmus v simulačním nástroji Plant Simulation. Na následujícím grafu je patrný vývoj vypočtené hodnoty účelové funkce (fitness) u jednotlivých provedených simulací. Optimalizace byla nastavena tak, že výpočet probíhá pro dvacet následných generací. V rámci jedné generace vznikne padesát nových potomků odvozených od svých rodičů. V tomto případě optimalizační nástroj potřeboval zhruba šest generací, než začal nacházet řešení blížící se k optimu. Dále je zde patrná skutečnost, že v jednotlivých generacích vznikají také v důsledku mutace nepříliš povedení potomci s vyšší hodnotou fitness, přičemž obecnou snahou je minimalizace hodnoty fitness jedince. Tento typ algoritmu dělá mutace záměrně, aby zkusil i jiná nastavení, která by ho mohla vést k lepšímu řešení.
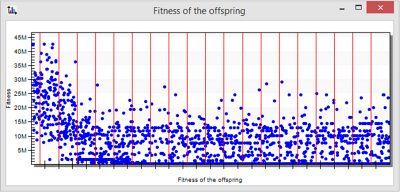
Graf 1
Po doběhnutí optimalizace je možné zobrazit seznam nejlepších nastavení vstupních parametrů (chromozom – v tabulce 1 není zobrazen). Řešení jsou vzestupně seřazena podle hodnoty fitness. V našem případě bylo nalezené nejlepší řešení obsaženo již v osmé generaci.
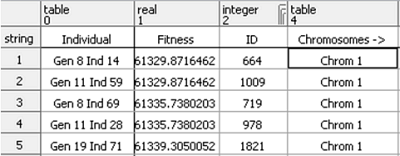
Tab. 1
Optimální rozmístění pracovišť
Na druhém příkladu lze demonstrovat použití optimalizace na simulačním modelu, pomocí něhož je hledáno optimální rozmístění osmi pracovišť. Optimalizačním kritériem je minimalizace celkově realizovaných přepravních vzdáleností. V modelu jsou vyráběny tři různé výrobky s využitím různých technologických postupů (viz tabulka 2). Výrobek A představuje čtyřicet procent celkové produkce, výrobek B se na celkové produkci podílí z 35 procent a výrobek C představuje 25 procent celkové produkce.
| Výrobek A 40% | Výrobek B 35% | Výrobek C 25% |
| Řezání | Řezání | Řezání |
| Soustružení | Frézovaní | Broušení |
| Frézovaní | Soustružení | Soustružení |
| Montáž 1 | Svařování | Frézovaní |
| Barvení | Broušení | Broušení |
| Montáž 2 | Barvení | Barvení |
| Broušení | Montáž 2 | Svařování |
| Expedice | Frézování | Frézování |
| Expedice | Expedice |
Výchozí rozmístění pracovišť se zobrazenou intenzitou toku všech vyráběných výrobků je znázorněno na obrázku 4. Z obrázku je patrné, že dochází k intenzivní přepravě na velké vzdálenosti mezi jednotlivými pracovišti. K optimalizaci je opět použit genetický algoritmus, který automaticky zkouší různé varianty rozmístění pracovišť. Pro výpočet hodnoty fitness jsou použity celkové náklady na transport.
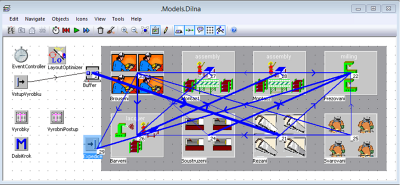
Obr. 4
V prvním kroku optimalizace se celkové přepravní náklady zmenšily ze třinácti na 8,5 milionu. Z obrázku 5 je patrné, že pracoviště se přemisťovala tak, aby došlo ke zmenšení vzdáleností mezi pracovišti s největší intenzitou toku. V druhém kroku optimalizace se celkové přepravní náklady podařilo snížit na 7,9 milionu. Projevilo se již pouze drobné zlepšení, a tuto variantu tudíž lze považovat za optimální řešení (obr. 6).
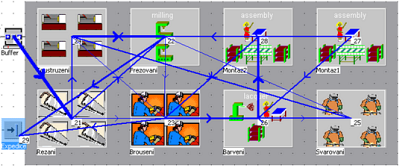
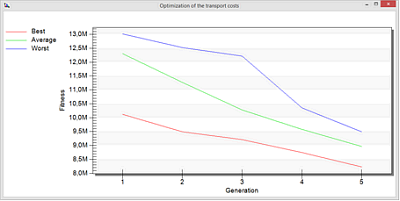
Obr. 5
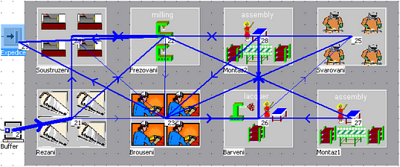
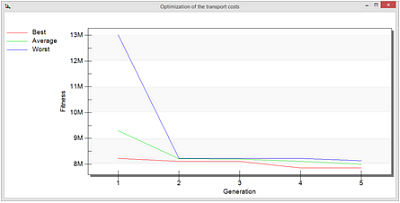
Obr. 6
Tento příklad je pouze ilustrací využití optimalizace při rozmisťování pracovišť. Je zcela pochopitelné, že obdobně jednoduchý příklad lze řešit také s využitím tzv. selského rozumu. V případě existence většího množství pracovišť, na kterých by bylo vyráběno větší množství různých výrobků, by pak nalezení optimálního rozmístění pracovišť alternativními způsoby bylo již značně problematické.
Závěr
Kromě zde uvedených příkladů jsou v oblasti logistiky dále vytvářeny následující typy simulačních modelů:
- systémy vychystávání zásob ze skladu,
- analýza materiálových toků ve výrobním systému,
- analýza vnitropodnikových dopravních systémů – dopravníky, AGV, vysokozdvižné vozíky apod.,
- řízení zásob materiálu,
- porovnání způsobů dopravy v podniku – AGV, vláček, VZV,
- analýza velikosti manipulačních dávek a použitých manipulačních jednotek (paleta versus KLT) atd.
Simulační studie jsou vytvářeny zejména s cílem nalezení takových podnikových opatření, která by vedla ke zvýšení produktivity práce při současné minimalizaci investičních a provozních nákladů. Jak již bylo uvedeno v předcházejícím článku publikovaném v IT Systems [1], lze díky závěrům ze simulačních studií pozitivně ovlivnit:
- zvýšení produkce,
- snížení prostojů (strojů, pracovníků),
- snížení počtu pracovníků,
- snížení rizika nedodržení termínů dokončení zakázek,
- ověření zamýšlených organizačních, řídicích a investičních záměrů a v důsledku toho eliminaci nesprávných rozhodnutí, která by v budoucnosti mohla vést k vnitropodnikovým problémům.
Při hledání optimálního nastavení výrobních a logistických procesů bývá často problémem příliš velké množství faktorů, které je třeba v podniku nastavit. V případně potřeby ověření veškerých možných nastavení by propočet všech možných variant řešení byl časově velmi náročný, někdy až nedosažitelný. Pro tyto účely lze využívat optimalizační nástroje, které se snaží automaticky nalézt vhodnou kombinaci nastavení systému při realizaci pokud možno co nejmenšího počtu provedených experimentů.
Zde uvedené přínosy vychází z mnoha praktických projektů, které byly realizovány jak pro podniky v oblasti automobilového průmyslu, tak i pro podniky mimo tuto oblast. Využity byly také zkušenosti dalších institucí působících v tomto oboru.
Zdroje
- Ulrych, Z., A. Miller. 2013. Simulace logistických toků a zásobování materiálem. IT Systems 2013, č. 11, s. 36-39.
- Dahl, O.J. 1966. Discrete Event Simulation Languages. Oslo: Norsk Regnesentral.
- Banks, J. et al. 2005. Discrete-Event System Simulation. Upper Saddle River: Pearson Prentice Hall.
- Ulrych, Z. et al. 2013. Simulace výrobních systémů a procesů. Plzeň: SmartMotion.
- Tvrdík, J. 2004. Virtuální informační centrum pro doktorandy informatiky. In: Evoluční algoritmy - učební texty [online].
Zdeněk Ulrych, Pavel Raška


Formulář pro přidání akce
| 13.3. | CONTROLLING A BI PRAKTICKY - Manažerská výsledovka |